Lowest Common Ancestor(LCA) Problems

Lowest Common Ancestor problems & solutions

Feb 10, 2025

Problem1: Lowest Common Ancestor of a Binary Search Tree

In the problem, we should find the common ancestor of p and q. Unlike in typical LCA problems, BST is used here, so we can take advantage of it.

If the current node is larger than p and q, it cannot be the ancestor. The right ancestor will be in the left tree.
If the current node is smaller than p and q, the answer should be in the right tree.
Otherwise, the current value should be the lowest common ancestor because one might be on the left and the other on the right. (Or the current node can be one of p and q)

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        while(true) {
            if(root->val < p->val && root->val < q->val) root = root->right;
            else if (root->val > p->val && root->val > q->val) root = root->left;
            else break;
        }
        return root;
    }
};

Problem2: Lowest Common Ancestor of a Binary Tree

Now, we should find the LCA from Binary Tree. This is not the BST, so we cannot decide which child node will contain the answer. It means that we should find the left and right child together.

The important thing is to determine which case can be the ancestor. Let’s say we already checked the left and right nodes.

If both the left and right nodes find something, the current node should be the common ancestor.
If not, there are two cases.
- 1) Find p or q, not both.
- 2) Find nothing.
- In both cases, the current node may be either p or q. If so, we can return it. The current node will be the answer if it is the first case. In the second case, the current node will indicate to the parent that it finds p or q.
If the current node is not p and q, then we can return the found node from the result of the left and right nodes.

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == nullptr) return nullptr;

        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);

        if ((left != nullptr && right != nullptr) || root == p || root == q) {
            return root;
        }

        return left == nullptr ? right : left;
    }
};

Problem3: Lowest Common Ancestor of Deepest Leaves

In this problem, we should find the LCA of deepest leaves. If there are more than 1 leaves that have the deepest depth, we should find the LCA for all of them. This is tricky, even though we search with DFS, we cannot know if it is the deepest leaves or not.

So, when we search the left and right nodes, we should get the deepest depth information as well. If the deepest depth of left tree is larger than that of right tree, then we should return LCA of left tree. It’s because the right tree must not be the answer. Of course, in this case, we are unsure that the LCA from left tree is the correct answer. There might be another LCA that has deeper depth.

To make the logic work, we should return the empty node’s depth with -1. This will work because if left node is empty and the right node is not, right node’s depth is always larger than that of the left node.

If the depth of left and right nodes are equal, then we should return the current node as the LCA. If it is the leaf node, then left and right node depth will be same and the value is -1. In this case, we should return the current depth to let parent know the deepest depth it has.

class Solution {
public:
    pair<TreeNode*, int> findLCADeepestLeaves(TreeNode* root, int depth) {
        if (root == nullptr) return {nullptr,  -1};

        auto left = findLCADeepestLeaves(root->left, depth + 1);
        auto right = findLCADeepestLeaves(root->right, depth + 1);

        if (left.second == right.second) {
            return {root, left.second == -1 ? depth : left.second };
        }
        return left.second < right.second ? right : left;
    }

    TreeNode* lcaDeepestLeaves(TreeNode* root) {
        return findLCADeepestLeaves(root, 0).first;
    }
};

Problem4: Lowest Common Ancestor of a Binary Tree II

This problem is a bit harder one than problem2. It’s because p or q might not be in the tree. We should return the LCA if and only if we find both of them in the tree.

Basic logic is the same as the problem2, but I added the boolean value that indicates returned node is the LCA. If it is false, then the node is just one of p or q, not the LCA.

If one of the left or right node found the answer, then we can return it. Unless, we should check the current node can be the answer.

If both left node and right node finds the LCA but those are not the answer, then p and q is found from different child. So the LCA of them is the current node.
If one of them finds the LCA and the current node is either p or q, then it also means that the current node is LCA.
In those two cases, the current node is the answer, so we should return true for the second return value.

Even though the current node is not the LCA, it can be one of p or q. If not, then the current node is useless, so return the non-empty node between left and right. (Both can be null, but it’s okay)

class Solution {
public:
    pair<TreeNode*, bool> lowestCommonAncestorHelper(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (!root) return {nullptr, false};

        auto left = lowestCommonAncestorHelper(root->left, p, q);
        auto right = lowestCommonAncestorHelper(root->right, p, q);
        if ((left.first != nullptr && right.first != nullptr) || ((root == p || root == q) && (left.first != nullptr || right.first != nullptr))) {
            return {root, true};
        }

        if (left.second) return left;
        if (right.second) return right;

        if (root == p || root == q) return {root, false};

        return left.first == nullptr ? right : left;
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        auto answer = lowestCommonAncestorHelper(root, p, q);
        return answer.second ? answer.first : nullptr;
    }
};

Problem5: Lowest Common Ancestor of a Binary Tree III

In this problem, we don’t know the root and only p and q are provided. However, each node has the parent infromation. So we can find the parent if we keep following the parent node.

To find the LCA, we can look through all parents of p and q.

Store all parents of p, including p itself until it reach to the root node.
Find the LCA by checking if the parent of q exists.
If nothing is found, then return nullptr.

class Solution {
public:
    Node* lowestCommonAncestor(Node* p, Node * q) {
        unordered_set<Node*> parents;
        while(p != nullptr) {
            parents.insert(p);
            p = p->parent;
        }
        while(q != nullptr) {
            if (parents.find(q) != parents.end()) return q;
            q = q->parent;
        }
        return nullptr;
    }
};

This problem can be solved without storing the parent information. No matter where p and q is located in the tree, they have each own depth from the root node. If the depth is equal, then we can simply iterate the parent one by one until both get the same parent.

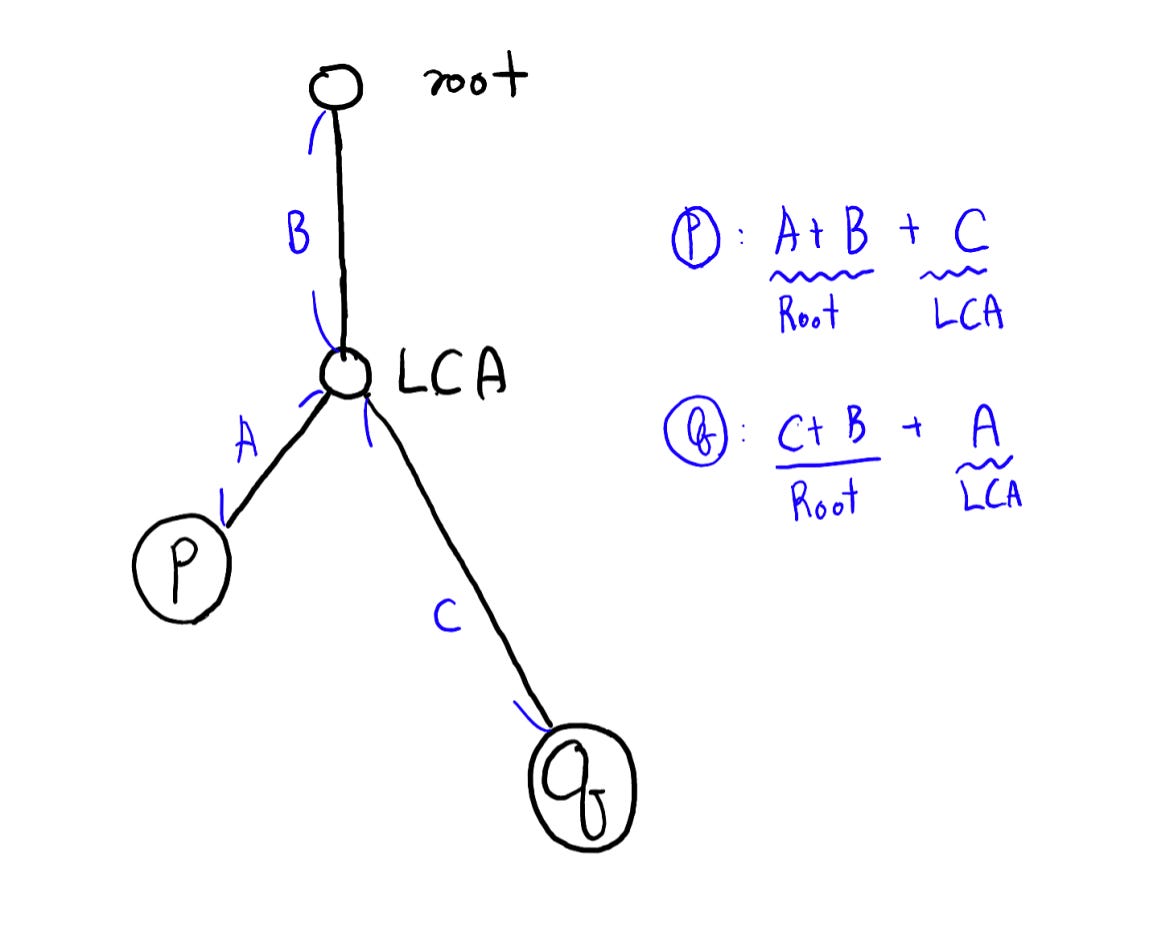
However, the problem happens when the depth is different. Let’s seem the following graph.

If p and q moves to each parent at the same speed, then the shorter one will arrive at the root node first. In this case, p is the shorter one and it will iterate A + B times. q also iterates A + B times. It is the C - A far from the root.
p is now starting again from original q position. Then it should iterate C times more to get to the LCA. However, before iterating C, q will arrive at the root node after C - A iteration. p also moves C - A times so it will be A far from the LCA.
if q starts from original p postion, both of them should move A times. In conclustion, both p and q moves A + B + C times to get to the LCA node.

class Solution {
public:
    Node* lowestCommonAncestor(Node* p, Node * q) {
        Node* l = p;
        Node* r = q;
        while(l != r) {
            l = l->parent == nullptr ? q : l->parent;
            r = r->parent == nullptr ? p : r->parent;
        }
        return l;
    }
};

Problem6: Lowest Common Ancestor of a Binary Tree IV

In this problem, we should find the LCA of multiple nodes. We can find all LCA one by one, but it will take too long time if array size is big. However, if you try to find the LCA with this method, then you will get one possible optimization idea.

Let’s assume that we find the LCA of A and B. (let’s call it X) If we want to find LCA of A,B,C, then we can find the LCA of X and C.

What if C is located in the child tree of X? In this case, we don’t need to consider C. It means that if we find a node, then we don’t need to think about the LCA of other nodes that are located in the child tree. So, we just can return the current node as the LCA.

So, the basic logic is mostly the same as the problem 2. One thing different is that, if the current node is in the list of nodes that we have to find, then we just can return the current node ans the LCA, no matter what result of left or right.

class Solution {
public:
    TreeNode* lowestCommonAncestorHelper(TreeNode* root, unordered_set<TreeNode*> & s) {
        if (root == nullptr) return nullptr;

        TreeNode* left = lowestCommonAncestorHelper(root->left, s);
        TreeNode* right = lowestCommonAncestorHelper(root->right, s);

        if ((left != nullptr && right != nullptr) || s.find(root) != s.end()) {
            return root;
        }

        return left == nullptr ? right : left;
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, vector<TreeNode*> &nodes) {
        unordered_set<TreeNode*> s;
        for (auto & node: nodes) s.insert(node);

        return lowestCommonAncestorHelper(root, s);
    }
};

Zero to Expert

Discussion about this post